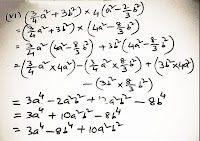NCERT Solutions for Class 8 Maths Chapter 9 Algebraic Expressions and Identities Ex 9.4
Algebraic Expressions and Identities: Here you get NCERT Solutions for Class 8 Maths Chapter 9 Algebraic Expressions and Identities Ex 9.4 with Answers Pdf free download.In NCERT Solution Class 8 Maths with Answers you get question-answer based on latest exam pattern. By providing NCERT Chapter-wise Class 6 Maths Questions with Answers our target to help students get concept of the lesson very well.
You can also visit NCERT Questions for Class 8 Maths Chapter-wise Questions with Answers to revise your syllabus thoroughly and enhance the chances of securing high marks in your board exams. It also helps in your CBSE NCERT Class 8 online test, online exam for admission well.
-------------------------------------------------------------
Board CBSE
-------------------------------------------------------------
TextBook NCERT
-------------------------------------------------------
CLASS Class 8
--------------------------------------------------------
SUBJECT Maths
----------------------------------------------------------
CHAPTER Chapter 9
-------------------------------------------------------------
SUBJECT Algebraic Expressions and Identities
--------------------------------------------------------------
Visit NCERT Solutions
Class 8 Maths Algebraic Expressions and Identities Exercise 9.1
Class 8 Maths Algebraic Expressions and Identities Exercise 9.2
Class 8 Maths Algebraic Expressions and Identities Exercise 9.3
Class 8 Maths Algebraic Expressions and Identities Exercise 9.4
Class 8 Maths Algebraic Expressions and Identities Exercise 9.5
You May Like
NCERT Solutions Class 8 Science
NCERT Solutions for Class 8 Maths Chapter 9 Algebraic Expressions and Identities Ex 9.4 with Answers
Exercise 9.4
Question 1.
Multiply the binomials:
(i) (2x + 5) and (4x – 3)
(ii) (y – 8) and (3y – 4)
(iii) (2.5l – 0.5m) and (2.5l + 0.5m)
(iv) (a + 3b) and (x + 5)
(v) (2pq + 3q2) and (3pq – 2q2)
(vi) (3/4a² + 3b²) and 4(a² – 2/3 b²)
Answer:
(i) (2x + 5) × (4x – 3)
= 2x (4x – 3) + 5 (4x – 3)
= (2x × 4x) – (3 × 2x) + (5 × 4x) – (5 × 3)
= 8x² – 6x + 20x – 15
= 8x² + 14x – 15
(ii) (y – 8) × (3y – 4)
= y (3y – 4) – 8 (3y – 4)
= (y × 3y) – (y × 4) – (8 × 3y) + (-8 × -4)
= 3y² – 4y – 24y + 32
= 3y² – 28y + 32
(iii) (2.5l – 0.5m) × (2.5l + 0.5m)
= (2.5l × 2.5l) + (2.5l × 0.5m) – (0.5m × 2.5l) – (0.5m × 0.5m)
= 6.25l² + 1.25ml – 1.25ml – 0.25m²
= 6.25l² + 0 – 0.25m²
= 6.25l² – 0.25m²
(iv) (a + 3b) × (x + 5)
= a (x + 5) + 36 (x + 5)
= (a × x) + (a × 5) + (36 × x) + (36 × 5)
= ax + 5a + 3bx + 15b
= ax + 3bx + 5a + 15b
(v) (2pq + 3q²) × (3pq – 2q²)
= 2pq × (3pq – 2q²) + 3q² (3pq – 2q²)
= (2pq × 3pq) – (2pq × 2q²) + (3q² × 3pq) – (3q² × 2q²)
= 6p²q² – 4pq³ + 9pq³ – 6q⁴
= 6p²q² + 5pq³ – 6q⁴
(vi)
Question 2.
Find the product:
(i) (5 – 2x) (3 + x)
(ii) (x + 7y) (7x – y)
(iii) (a2 + b) (a + b2)
(iv) (p2 – q2)(2p + q)
Answer:
(i) (5 – 2x) (3 + x)
= 5(3 + x) – 2x(3 + x)
= (5 × 3) + (5 × x) – (2x × 3) – (2x × x)
= 15 + 5x – 6x – 2x²
(ii) (x + 7y) (7x – y)
= x(7x – y) + 7y(7x – y)
= (x × 7x) – (x × y) + (7y × 7x) – (7y × y)
= 7x² – xy + 49xy – 7y²
= 7x² + 48xy – 7y²
(iii) (a² + b) (a + b²)
= a²(a + b2) + b(a + b²)
= (a² × a) + (a² × b²) + (b × a) + (b × b²)
= a³ + a²b² + ab + b³
(iv) (p² – q²)(2p + q)
= p²(2p + q) – q²(2p + q)
= (p² × 2p) + (p² × q) – (q² × 2p) – (q² × q)
= 2p³+ p²q – 2pq² – q³
Question 3.
Simplify:
(i) (x² – 5) (x + 5) + 25
(ii) (a² + 5)(b³ + 3) + 5
(iii) (t + s³) (t² – s)
(iv) (a + b) (c – d) + (a – b) (c + d) + 2(ac + bd)
(v) (x + y) (2x + y) + (x + 2y) (x – y)
(vi) (x + y)(x² – xy + y²)
(vii) (1.5x – 4y)(1.5x + 4y + 3) – 4.5x + 12y
(viii) (a + b + c) (a + b – c)
Answer:
(i) (x² – 5) (x + 5) + 25
= x²(x + 5) - 5(x + 5) + 25
= x³ + 5x² – 5x – 25 + 25
= x³ + 5x² – 5x + 0
= x³ + 5x² – 5x
(ii) (a² + 5)(b³ + 3) + 5
= a²(b³ + 3) + 5(b³+ 3) + 5
= a²b³+ 3a² + 5b³ + 15 + 5
= a²b³ + 3a² + 5b³ + 20
(iii) (t + s²) (t² – s)
= t(t² – s) + s²(t² – s)
= t³ – st + s²t²– s³
= t³ + s²t² – st – s³
(iv) (a + b)(c – d) + (a – b) (c + d) + 2(ac + bd)
= a(c – d) + b(c – d) + a(c + d) – b(c + d) + 2ac + 2bd
= ac – ad + bc – bd + ac + ad – bc – bd + 2ac + 2bd
= (ac + ac + 2ac) + (bc – bc) – (ad + ad) – (bd – bd + 2bd)
= 4ac + 0 + 0 + 0
= 4ac
(v) (x + y) (2x + y) + (x + 2y) (x – y)
= x(2x + y) + y(2x + y) + x(x – y) + 2y(x – y)
= 2x² + xy + 2xy + y² + x² – xy + 2xy – 2y²
= (2x² + x²) + (xy + 2xy – xy + 2xy) +( y² – 2y²)
= 3x² + 4xy – y²
(vi) (x + y)(x² – xy + y²)
= x(x² – xy + y²) + y(x² – xy + y²)
= x³ – x²y + x²y + xy² – xy² + y³
= x³ + (x²y - x²y) + (xy² - xy²) + y³
= x³ – 0 + 0 + y³
= x³ + y³
(vii) (1.5x – 4y)(1.5x + 4y + 3) – 4.5x.+ 12y
= 1.5x (1.5x + 4y + 3) – 4y(1.5x + 4y + 3) – 4.5x + 12y
= 2.25x² + 6xy + 4.5x – 6xy – 16y² – 12y – 4.5x + 12y
= 2.25x² + 6xy – 6xy + 4.5x – 4.5x + 12y – 12y – 16y²
= 2.25x² + 0 + 0 + 0 – 16y²
= 2.25x² – 16y²
(viii) (a + b + c) (a + b – c)
= a(a + b – c) + b(a + b – c) + c(a + b – c)
= a² + ab – ac + ab + b² – bc + ac + bc – c²
= a² + ab + ab – bc + bc – ac + ac + b² – c²
= a² + 2ab + b² – c² + 0 + 0
= a² + 2ab + b² – c²
= a² +b² - c² + 2ab
NCERT Solutions for Class 8 Maths Chapter 9 Algebraic Expressions and Identities Ex 9.4 with Answers