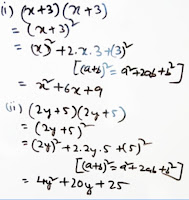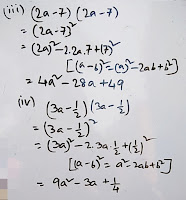NCERT Solutions for Class 8 Maths Chapter 9 Algebraic Expressions and Identities Ex 9.5
Algebraic Expressions and Identities: Here you get NCERT Solutions for Class 8 Maths Chapter 9 Algebraic Expressions and Identities Ex 9.5 with Answers Pdf free download.In NCERT Solution Class 8 Maths with Answers you get question-answer based on latest exam pattern. By providing NCERT Chapter-wise Class 6 Maths Questions with Answers our target to help students get concept of the lesson very well.
You can also visit NCERT Questions for Class 8 Maths Chapter-wise Questions with Answers to revise your syllabus thoroughly and enhance the chances of securing high marks in your board exams. It also helps in your CBSE NCERT Class 8 online test, online exam for admission well.
-------------------------------------------------------------
Board CBSE
-------------------------------------------------------------
TextBook NCERT
-------------------------------------------------------
CLASS Class 8
--------------------------------------------------------
SUBJECT Maths
----------------------------------------------------------
CHAPTER Chapter 9
-------------------------------------------------------------
SUBJECT Algebraic Expressions and Identities
--------------------------------------------------------------
Visit NCERT Solutions
Class 8 Maths Algebraic Expressions and Identities Exercise 9.1
Class 8 Maths Algebraic Expressions and Identities Exercise 9.2
Class 8 Maths Algebraic Expressions and Identities Exercise 9.3
Class 8 Maths Algebraic Expressions and Identities Exercise 9.4
Class 8 Maths Algebraic Expressions and Identities Exercise 9.5
You May Like
NCERT Solutions Class 8 Science
NCERT Solutions for Class 8 Maths Chapter 9 Algebraic Expressions and Identities Ex 9.5 with Answers
Exercise 9.5
Question 1.
Use a suitable identity to get each of the following products:
(i) (x + 3) (x + 3)
(ii) (2y + 5) (2y + 5)
(iii) (2a – 7) (2a – 7)
(iv) (3a – 1/2) (3a – 1/2)
(v) (1.1m – 0.4) (1.1m + 0.4)
(vi) (a² + b²) (-a² + b²)
(vii) (6x – 7) (6x + 7)
(viii) (-a + c) (-a + c)
(ix) (x/2 + 3y/4) (x/2 + 3y/4)
(x) (7a – 9b) (7a – 9b)
Answer:
Question 2.
Use the identity (x + a)(x + b) = x² + (a + b)x + ab to find the following products.
(i) (x + 3) (x + 7)
(ii) (4x + 5)(4x + 1)
(iii) (4x – 5) (4x – 1)
(iv) (4x + 5) (4x – 1)
(v) (2x + 5y) (2x + 3y)
(vi) (2a² + 9) (2a² + 5)
(vii) (xyz – 4) (xyz – 2)
Answer:
Question 3.
Find the following squares by using the identities.
(i) (b – 7)²
(ii) (xy + 3z)²
(iii) (6x² – 5y)²
(iv) {(⅔)m + (3/2) n}²
(v) (0.4p – 0.5q)²
(vi) (2xy + 5y)²
Answer:
Question 4.
Simplify:
(i) (a² – b²)²
(ii) (2x + 5)² – (2x – 5)²
(iii) (7m – 8n)² + (7m + 8n)²
(iv) (4m + 5n)² + (5m + 4n)²
(v) (2.5p – 1.5q)² – (1.5p – 2.5q)²
(vi) (ab + bc)² – 2ab²c
(vii) (m² – n²m)² + 2m³n²
Answer:
Question 5.
Show that:
(i) (3x + 7)² – 84x = (3x – 7)²
(ii) (9p – 5q)² + 180pq = (9p + 5q)²
(iii) (4/3 m – 3/4 n)² + 2mn = 16/9 m² + 91/6 n2
(iv) (4pq + 3q)² – (4pq – 3q)² = 48pq²
(v) (a – b)(a + b) + (b – c) (b + c) + (c – a) (c + a) = 0
Answer:
Question 6.
Using identities, evaluate:
(i) 71²
(ii) 99²
(iii) 102²
(iv) 998²
(v) 5.2²
(vi) 297 × 303
(vii) 78 × 82
(viii) 8.9²
(ix) 1.05 × 9.5
Answer:
Question 7.
Using a² – b² = (a + b) (a – b), find
(i) 51² – 49²
(ii) (1.02)² – (0.98)²
(iii) 153² – 147²
(iv) 12.1² – 7.9²
Answer:
(i) 51² – 49²
= (51 + 49) (51 – 49)
= 100 × 2
= 200
(ii) (1.02)² – (0.98)²
= (1.02 + 0.98) (1.02 – 0.98)
= 2.00 × 0.04
= 0.08
(iii) 153² – 147²
= (153 + 147) (153 – 147)
= 300 × 6
= 1800
(iv) 12.1² – 7.9²
= (12.1 + 7.9) (12.1 – 7.9)
= 20.0 × 4.2
= 84
Question 8.
Using (x + a) (x + b) = x² + (a + b)x + ab, find
(i) 103 × 104
(ii) 5.1 × 5.2
(iii) 103 × 98
(iv) 9.7 × 9.8
Answer:
(i) 103 × 104
= (100 + 3)(100 + 4)
= (100)² + (3 + 4) (100) + (3 × 4)
= 10000 + 700 + 12
= 10712
(ii) 5.1 × 5.2
= (5 + 0.1) (5 + 0.2)
= (5)² + (0.1 + 0.2) (5) + (0.1 × 0.2)
= 25 + 1.5 + 0.02
= 26.5 + 0.02
= 26.52
(iii) 103 × 98
= (100 + 3) (100 – 2)
= (100)² + (3 – 2) (100) + 3 × (-2)
= 10000 + 100 – 6
= 10100 – 6
= 10094
(iv) 9.7 × 9.8
= (10 – 0.3) (10 – 0.2)
= (10)² – (0.3 + 0.2) (10) + (-0.3) (-0.2)
= 100 – 5 + 0.06
= 95 + 0.06
= 95.06