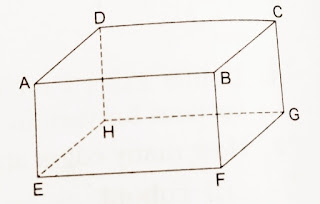
Volume and Surface Area of Solids : Cuboid, Class 8 CBSE NCERT
1. Question
Find the volume, lateral surface area and the total surface area of the cuboid whose dimensions are:
(i) length = 22 cm, breadth = 12 cm and height = 7.5 cm
Answer
(i) We know that,
Volume of cuboid = Length × Breadth × Height
= (22 × 12 × 7.5)
= 1980 cm3
We also know that,
Total Surface Area of cuboid = 2 (lb + bh + hl)
= 2 (22 × 12) + (22 × 7.5) + (12 × 7.5)
= 2 (264 + 165 + 90)
= 1038 cm²
Now,
Lateral surface area of cuboid = [2 (l + b) × h]
= [2 (22 + 12) × 7.5]
= 510 cm²
(ii) length = 15 m, breadth = 6 m and height = 9 dm
Answer:
We know that,
Volume of cuboid = Length × Breadth × Height
= (15 × 6 × 0.9)
= 81 m³
Total Surface Area of cuboid = 2 (lb + bh + hl)
= 2 (15 × 6) + (15 × 0.9) + (6 × 0.9)
= 2 (90 + 13.5 + 5.4)
= 217.8 m²
Lateral surface area of cuboid = [2 (l + b) × h]
= 2 (15 + 6) × 0.9
= 37.8 m²
(iii) length = 24 m, breadth = 25 cm and height = 6 m
Answer:
Volume of cuboid = Length × Breadth × Height
= (24 × 0.25 × 6)
= 36 m³
Total Surface Area of cuboid = 2 (lb + bh + hl)
= 2 (24 × 0.25) + (24 × 6) + (0.25 × 6)
= 2 (6 + 144 + 1.5)
= 303 m²
Lateral surface area of cuboid = [2 (l + b) × h]
= 2 (24 + 0.25) × 6
= 291 m²
2. Question
The dimensions of a rectangular water tank are 2 m 75 cm by 1 m 80 cm by 1 m 40 cm. How many litres of
water does it hold when filled to the brim?
Answer
We know,
1m = 100 cm
Therefore,
Dimensions of the tank will be: 2m 75cm × 1m 80 cm × 1m 40cm
= 275 cm × 180 cm × 140 cm
We know,
Volume of the cuboid =( Length × Breadth × Height)
= 275 × 180 × 140
= 6930000 cm3
We know,
1000 cm3 = 1L
Therefore,
Volume =6930000/1000
= 6930 Litres
3. Question
A solid rectangular piece of iron measures 1.05 m x 70 cm x 1.5 cm. Find the weight of this piece in
kilograms if 1 cm3 of iron weighs 8 grams.
Answer
We know ,
1m = 100cm
Dimensions of the iron piece will be: 105 cm × 70 cm × 1.5 cm
We know,
Volume of cuboid =( Length × Breadth × Height)
Total volume of the piece of iron =( 105 × 70 × 1.5)
= 11025 cm3
We know
1 cm³= 8 gms
Weight of the piece = 11025 × 8
= 88200 g
=88200/1000
= 88.2 kg
4. Question
The area of a courtyard is 3750 m². Find the cost of covering it with gravel to a height of 1 cm if the gravel
costs Rs. 6.40 per cubic metre.
Answer
We know that,
1cm = 0.01m
Volume of the gravel used = Area × Height
= 3750 × 0.01
= 37.5 m³
The cost of the gravel is Rs. 6.40 per cubic meter
Therefore,
Total cost of covering = (37.5 × 6.4)
= Rs. 240
5. Question
How many persons can be accommodated in a hall of length 16 m, breadth 12.5 m and height 4.5 m,
assuming that 3.6 m³ of air is required for each person?
Answer
We know ,
Volume of cuboid = Length × Breadth × Height
Therefore,
Total volume of the hall = 16 × 12.5 × 4.5
= 900 m³
3.6 m³ of air is required for each person
Therefore,
number of persons that can be accommodated in the hall =
=900/3.6
= 250 people
6. Question
A cardboard box is 1.2 m long, 72 cm wide and 54 cm high. How many bars of soap can be put into it if each
bar measures 6 cm x 4.5 cm x 4 cm?
Answer
We know ,
Volume of cuboid = Length × Breadth × Height
Volume of cardboard box = 120 × 72 × 54
= 466560 cm³
Volume of each bar of soap = 6 × 4.5 × 4
= 108 cm³
Total number of bars of soap that can be accommodated in that box =
=466560/108
= 4320 bars
7. Question
The size of a matchbox is 4 cm x 2.5 cm x 1.5 cm. What is the volume of a packet containing 144
matchboxes? How many such packets can be placed in a carton of size 1.5 m x 84 cm x 60 cm?
Answer
We know,
Volume of cuboid = Length × Breadth × Height
Volume occupied by a single matchbox = (4 × 2.5 × 1.5)
= 15 cm³
Now,
Volume of a packet containing 144 matchboxes = (15 × 144)
= 2160 cm³
If,
Volume of carton = (150 × 84 × 60)
= 756000 cm³
Therefore,
Total number of packets that can be placed in a carton =756000/2160
= 350 packets
8. Question
How many planks of size 2 m x 25 cm x 8 cm can be prepared from a wooden block 5 m long, 70 cm broad
and 32 cm thick, assuming that there is no wastage?
Answer
Volume of cuboid = Length × Breadth × Height
Total volume of the block = (500 × 70 × 32)
= 1120000 cm³
Total volume of each plank = 200 × 25 × 8
= 40000 cm³
Hence,
Total number of planks that can be made =1120000/40000
= 28 planks
9. Question
How many bricks, each of size 25 cm x 13.5 cm x 6 cm, will be required to build a wall 8 m long, 5.4 m high
and 33 cm thick?
Answer
Volume of cuboid = Length × Breadth × Height
Volume ofone brick = 25 × 13.5 × 6
= 2025 cm³
Now,
Volume of the wall = 800 × 540 × 33
= 14256000 cm³
Hence,
Total number of bricks required
=14256000/2025
= 7040 bricks
10. Question
A wall 15 m long, 30 cm wide and 4 m high is made of bricks, each measuring 22 cm x 12.5 cm x 7.5 cm. If
of the total volume of the wall consists of mortar, how many 12bricks are there in the wall?
Hint. Volume of bricks in the wall = {(1500 x 30 x 400) x (1500 x 30 x 400)1 cm3.
Answer
Volume of cuboid = Length × Breadth × Height
So, Volume of the wall = 1500 × 30 × 400
= 18000000 cm3
Total quantity of mortar =
= 1500000 cm3
Therefore,
Volume of bricks = 18000000 – 1500000
= 16500000 cm3
Now,
Volume of a single brick = 22 × 12.56 × 7.5
= 2062.5 cm3
Therefore,
Total number of bricks
=16500000/2062.5
= 8000 bricks
11. Question
Find the capacity of a rectangular cistern in litres whose dimensions are 11.2 m x 6 m x 5.8 m. Find the area
of the iron sheet required to make the cistern.
Answer
Volume of cuboid = Length × Breadth × Height
Volume of the cistern = 11.2 × 6 × 5.8
= 389.76 m³
1m³=1000 litres
= 389.76 × 1000
= 389760 litres
Now,
Area of iron sheet that is needed to make the cistern = Total surface area of the cistern
We also know that,
Total Surface Area of cuboid = 2 (lb + bh + hl)
= 2 (11.2 × 6 + 11.2 × 5.8 + 6 × 5.8)
= 2 (67.2 + 64.96 + 34.8)
= 333.92 cm²
12. Question
The volume of a block of gold is 0.5 m³. If it is hammered into a sheet to cover an area of 1 hectare, find the
thickness of the sheet.
Answer
Volume of the block = 0.5 m3
We know,
1 hectare = 10000 m²
So,
Thickness of the sheet = volume/area
= 0.5/10000
= 0.00005 m
= 0.005 cm
= 0.05 mm
For more questions click here