Volume and Surface Area of Solids : Formula and Solution class 8

 The surface area is the area that describes the material that will be used to cover a geometric solid. When we determine the surface areas of a geometric solid we take the sum of the area for each geometric form within the solid. The volume is a measure of how much a figure can hold and is measured in cubic units.

The  bodies that have a definite shape and volume are called solids.  The space occupied by a solid body is called its volume. 

 solid bodies occur in solid bodies occur in various shapes such as cuboids cubes cylinder cones and spheres. 

Cuboid:  a solid bounded by six rectangular plane faces is called a cuboid. 

Example: a matchbox, chalk box, a brick, a title,  a book.

Cuboid has 6 rectangular faces, 12 edges, 8 vertices. 

 any face of any face of a cuboid maybe called its base. 

 the four faces which meet the base are the four faces which meet the base are called lateral faces of the cuboid. 

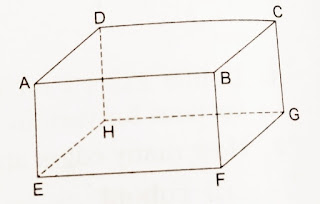
 6 faces are ABCD, EFGH, 

EFBA, HGCD, EHDA, FGCB

12 edgess are AE, DH, BF, CG, AD, EH, FG, BC, AB, CD, EF, GH

8 vertics are A, B, C, D, E, F, G, H. 

 

CUBE: A   cuboid whose Length breadth and height are all equal is called a cube.  

Example: ice cubes, dice, sugar cubes.

 

Formula  for volume and surface area of cuboid and cube 

Cuboid: 

i) volume of a cuboid= (length × breadth × height)  = ( l × b × h)

ii) Diagonal of a cuboid = √(l² × b² ×h² )

iii)  total surface area of a cuboid= 2 (lb × bh × lh)

iv) lateral surface area of a cuboid = [2 ( l×b ) × h]

CUBE

i) volume of a cube = (side) ³ = a³

ii) diagonal of a cube = √3a

iii) total surface area of a cube= 6a²

iv)  lateral surface area of a cube= 4a²

 

PROBLEMS ON CUBOID (CLICK HERE)