NCERT Solution for Class 8 Math: Cube and Cube Roots
In NCERT Solution of Class 8 of math chapter 7 Cube and Cube Roots get worksheet, questions answers,solve paper.
Question 1:
Which of the following numbers are not perfect cubes:
(i) 216 (ii) 128 (iii) 1000 (iv) 100 (v) 46656
Answer 1:
(i) 216
Prime factors of 216 = 2 x 2 x 2 x 3 x 3 x 3
Since all factors are in groups of 3’s (in triplets)
Therefore, 216 is a perfect cube number.
(ii) 128
Prime factors of 128 = 2 x 2 x 2 x 2 x 2 x 2 x 2
Number of 2's = 7
Since, one factor 2 does not appear in a 3’s group.
Therefore, 128 is not a perfect cube.
(iii) 1000
Prime factors of 1000 = 2 x 2 x 2 x 3 x 3 x 3
Number of 2's =3 and Number of 3's=3
Since, all factors appear in 3’s group.
Hence, 1000 is a perfect cube.
(iv) 100
Prime factors of 100 = 2 x 2 x 5 x 5
Number of 2's=2 and Number of 5's= 3
Since, all factors do not appear in 3’s group.
Hence, 100 is not a perfect cube.
(v) 46656
Prime factors of 46656 = 2 x 2 x 2 x 2 x 2 x 2 x 3 x 3 x 3 x 3 x 3 x 3
Number of 2'=6 and Number of 3's=6
Since, all factors appear in 3’s group.
Hence, 46656 is a perfect cube.
Question 2:
Find the smallest number by which each of the following numbers must be multiplied to obtain a perfect cube:
(i) 243 (ii) 256(iii) 72 (iv) 675 (v) 100
Answer 2:
(i) 243
Prime factors of 243 = 3 x 3 x 3 x 3 x 3
Number of 3's=5
Here 3 does not appear in 3’s group. To make group of 3's we should multiplied one more 3.
Therefore, 243 must be multiplied by 3 to make it a perfect cube.
(ii) 256
Prime factors of 256 = 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2
Number of 2'=8
Here 2 does not appear in 2’s group. To make group of 2's we should multiplied one more 2.
Therefore, 256 must be multiplied by 2 to make it a perfect cube
(iii) 72
Prime factors of 72 = 2 x 2 x 2 x 3 x 3
Number of 2'=3 and Number of 3'=3
Here 3 does not appear in 3’s group.To make it in group 3's we should multiplied one more 3
Therefore, 72 must be multiplied by 3 to make it a perfect cube
(iv) 675
Prime factors of 675 = 3 x 3 x 3 x 5 x 5
Number of 3's=3 and Number of 5's=2
Here factor 5 does not appear in 3’s group. To make it group of 3's we should multiplied one more 5
Therefore 675 must be multiplied by 5 to make it a perfect cube.
(v) 100
Prime factors of 100 = 2 x 2 x 5 x 5
Number of 2'=2 and Number of 5's=2
Here factor 2 and 5 both do not appear in 3’s group. To make 2 and 5 in we need to multiplied one more 2 and 5
Therefore 100 must be multiplied by 2 x 5 = 10 to make it a perfect cube.
Question 3:
Find the smallest number by which each of the following numbers must be divided to obtain a perfect cube:
(i) 81 (ii) 128 (iii) 135 (iv) 192 (v) 704
Answer 3:
(i) 81
Prime factors of 81 = 3 x 3 x 3 x 3
Number of 3'=4
Here one factor 3 is not group of 3's. To make it group of 3's we should divide it by one 3.
Therefore 81 must be divided by 3 to make it a perfect cube.
(ii) 128
Prime factors of 128 = 2 x 2 x 2 x 2 x 2 x 2 x 2
Number of 2's=7
Here one factor 2 does not appear in a 3’s group. To make it group of 3's we should divide it by one 2.
Therefore, 128 must be divided by 2 to make it a perfect cube.
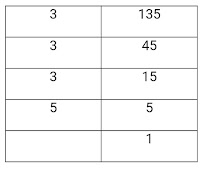
(iii) 135
Prime factors of 135 = 3 x 3 x 3 x 5
Number of 3's=3 and Number of 5'=1
Here one factor 5 does not in group of 3's. We should divide this 5 to make it perfect square.
Therefore, 135 must be divided by 5 to make it a perfect cube
(iv) 192
Prime factors of 192 = 2 x 2 x 2 x 2 x 2 x 2 x 3
Number of 2'=6 and Number of 3's=1
Here one factor 3 does not appear in group of 3's. We should divide it.
Therefore, 192 must be divided by 3 to make it a perfect cube.
(v) 704
Prime factors of 704 = 2 x 2 x 2 x 2 x 2 x 2 x 11
Number of 2's=6 and Number of 11=1
Here one factor 11 does not appear in group of 3's. We should divide it.
Therefore, 704 must be divided by 11 to make it a perfect cube.
Question 4:
Parikshit makes a cuboid of plasticine of sides 5 cm, 2 cm, 5 cm. How many such cuboids will he need to form a cube?
Answer 4:
Given numbers = 5 x 2 x 5
Number of 5's=2 and Number of 2's=1
Since, Factors of 5 and 2 both are not in group of three.
Therefore, the number must be multiplied by 2 x 2 x 5 = 20 to make it a perfect cube.
Hence he needs 20 cuboids.
Exercise:-7.2
Question 1:
Find the cube root of each of the following numbers by prime factorization method:
(i) 64 (ii) 512 (iii) 10648 (iv) 27000 (v) 15625 (vi) 13824 (vii) 110592 (viii) 46656
(ix) 175616 (x) 91125
Answer 1:
Question 2:
State true or false:
(i) Cube of any odd number is even.
Answer: false.
Correct statement: cube of any odd number is odd. Such as: 3³=9, 5³=125
(ii) A perfect cube does not end with two zeroes.
Answer: true.
(Such as: 10³=1000, 20³= 8000, always end with three 0.)
(iii) If square of a number ends with 5, then its cube ends with 25.
Answer: false
(Such as: Case I: 5²=25 and 5³=125 here ends with 25.
Case Ii: 15²=225 and 15³= 3375 here ends with 75) For More learn
(iv) There is no perfect cube which ends with 8.
Answer: false
(Such as 12³=1728 ends with 8)
(v) The cube of a two digit number may be a three digit number.
Answer: false
(Because the smallest two digit number is 10 and it's cube, 10³= 1000, which is a four digit number.)
(vi) The cube of a two digit number may have seven or more digits.
Answer: false
(Because the largest two digit number is 99 and it's cube 99³=970299, which is a 6 digit number)
(vii) The cube of a single digit number may be a single digit number.
Answer: true.
(Such as 2³=8 is a one digit number
4³=16 is a two digit number)
Question 3:
You are told that 1,331 is a perfect cube. Can you guess with factorization what is its cube root? Similarly guess the cube roots of 4913, 12167, 32768.
Answer 3:
(i) First we divide the digits into group of three digits from rightmost side. Now we get two groups. First group has digit 331 and second group has digit 1.
Since fast group has 1 in its unit place so the cube root number has digit 1 at its unit place because 1³=1
In second group the number is 1. We know that 1³=1
Therefore the digit of 10 place of cube root number is 1
Hence cube root of 1331 is 11
(learn how to cube number)
(ii) cube root of number 4913?
First we divide the digits into groups of three digit. Now we get two groups, first group has number 913 and second group has number only 4.
Since there is 3 at unit place of 913 therefore the cube root number has 7 in its unit place because 7³=343.
The second group has number 4. Now 1³=1, 2³=8. 1 < 4 < 8. Since 1 is nearer to 4 then 8. Therefore what is the digit at tens place of cube root number.
Therefore cube root of 4913 is 17.
(iii) 12167
We divide the digits into group of three digits
We get two groups. First group has number 167 and second group has number 12.
Since there is seven at one place in first group so so there is 3 at one's place of the cube root number because 3³=27.
In second group there is the number 12. 2³=8 and 3³=27.
8 < 12 < 27
8 is nearer to 12 then 27. Therefore at 10 place there is 2 of cube root number.
Hence the cube root of number 12167 is 23
(iv) 32768
first we divide the digits into groups of three digits. We get two groups. First group has number 768 and second group has number 32.
since there is 8 at one place of first group number so there is two at unit place of cube root number because 2³=8.
Second group has number 32.
3³=27,. 4³=64
27 < 32 < 64
27 is nearer to 32 than 64.
Therefore there is 3 at ten place of cube root number.
Hence the cube root number of 32768 is 32.
Question 1:
Which of the following numbers are not perfect cubes:
(i) 216 (ii) 128 (iii) 1000 (iv) 100 (v) 46656
Answer 1:
(i) 216
Prime factors of 216 = 2 x 2 x 2 x 3 x 3 x 3
Since all factors are in groups of 3’s (in triplets)
Therefore, 216 is a perfect cube number.
(ii) 128
Prime factors of 128 = 2 x 2 x 2 x 2 x 2 x 2 x 2
Number of 2's = 7
Since, one factor 2 does not appear in a 3’s group.
Therefore, 128 is not a perfect cube.
(iii) 1000
Prime factors of 1000 = 2 x 2 x 2 x 3 x 3 x 3
Number of 2's =3 and Number of 3's=3
Since, all factors appear in 3’s group.
Hence, 1000 is a perfect cube.
(iv) 100
Prime factors of 100 = 2 x 2 x 5 x 5
Number of 2's=2 and Number of 5's= 3
Since, all factors do not appear in 3’s group.
Hence, 100 is not a perfect cube.
(v) 46656
Prime factors of 46656 = 2 x 2 x 2 x 2 x 2 x 2 x 3 x 3 x 3 x 3 x 3 x 3
Number of 2'=6 and Number of 3's=6
Since, all factors appear in 3’s group.
Hence, 46656 is a perfect cube.
Question 2:
Find the smallest number by which each of the following numbers must be multiplied to obtain a perfect cube:
(i) 243 (ii) 256(iii) 72 (iv) 675 (v) 100
Answer 2:
(i) 243
Prime factors of 243 = 3 x 3 x 3 x 3 x 3
Number of 3's=5
Here 3 does not appear in 3’s group. To make group of 3's we should multiplied one more 3.
Therefore, 243 must be multiplied by 3 to make it a perfect cube.
(ii) 256
Prime factors of 256 = 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2
Number of 2'=8
Here 2 does not appear in 2’s group. To make group of 2's we should multiplied one more 2.
Therefore, 256 must be multiplied by 2 to make it a perfect cube
(iii) 72
Prime factors of 72 = 2 x 2 x 2 x 3 x 3
Number of 2'=3 and Number of 3'=3
Here 3 does not appear in 3’s group.To make it in group 3's we should multiplied one more 3
Therefore, 72 must be multiplied by 3 to make it a perfect cube
(iv) 675
Prime factors of 675 = 3 x 3 x 3 x 5 x 5
Number of 3's=3 and Number of 5's=2
Here factor 5 does not appear in 3’s group. To make it group of 3's we should multiplied one more 5
Therefore 675 must be multiplied by 5 to make it a perfect cube.
(v) 100
Prime factors of 100 = 2 x 2 x 5 x 5
Number of 2'=2 and Number of 5's=2
Here factor 2 and 5 both do not appear in 3’s group. To make 2 and 5 in we need to multiplied one more 2 and 5
Therefore 100 must be multiplied by 2 x 5 = 10 to make it a perfect cube.
Question 3:
Find the smallest number by which each of the following numbers must be divided to obtain a perfect cube:
(i) 81 (ii) 128 (iii) 135 (iv) 192 (v) 704
Answer 3:
(i) 81
Prime factors of 81 = 3 x 3 x 3 x 3
Number of 3'=4
Here one factor 3 is not group of 3's. To make it group of 3's we should divide it by one 3.
Therefore 81 must be divided by 3 to make it a perfect cube.
(ii) 128
Prime factors of 128 = 2 x 2 x 2 x 2 x 2 x 2 x 2
Number of 2's=7
Here one factor 2 does not appear in a 3’s group. To make it group of 3's we should divide it by one 2.
Therefore, 128 must be divided by 2 to make it a perfect cube.
(iii) 135
Prime factors of 135 = 3 x 3 x 3 x 5
Number of 3's=3 and Number of 5'=1
Here one factor 5 does not in group of 3's. We should divide this 5 to make it perfect square.
Therefore, 135 must be divided by 5 to make it a perfect cube
(iv) 192
Prime factors of 192 = 2 x 2 x 2 x 2 x 2 x 2 x 3
Number of 2'=6 and Number of 3's=1
Here one factor 3 does not appear in group of 3's. We should divide it.
Therefore, 192 must be divided by 3 to make it a perfect cube.
(v) 704
Prime factors of 704 = 2 x 2 x 2 x 2 x 2 x 2 x 11
Number of 2's=6 and Number of 11=1
Here one factor 11 does not appear in group of 3's. We should divide it.
Therefore, 704 must be divided by 11 to make it a perfect cube.
Question 4:
Parikshit makes a cuboid of plasticine of sides 5 cm, 2 cm, 5 cm. How many such cuboids will he need to form a cube?
Answer 4:
Given numbers = 5 x 2 x 5
Number of 5's=2 and Number of 2's=1
Since, Factors of 5 and 2 both are not in group of three.
Therefore, the number must be multiplied by 2 x 2 x 5 = 20 to make it a perfect cube.
Hence he needs 20 cuboids.
Exercise:-7.2
Question 1:
Find the cube root of each of the following numbers by prime factorization method:
(i) 64 (ii) 512 (iii) 10648 (iv) 27000 (v) 15625 (vi) 13824 (vii) 110592 (viii) 46656
(ix) 175616 (x) 91125
Answer 1:
Question 2:
State true or false:
(i) Cube of any odd number is even.
Answer: false.
Correct statement: cube of any odd number is odd. Such as: 3³=9, 5³=125
(ii) A perfect cube does not end with two zeroes.
Answer: true.
(Such as: 10³=1000, 20³= 8000, always end with three 0.)
(iii) If square of a number ends with 5, then its cube ends with 25.
Answer: false
(Such as: Case I: 5²=25 and 5³=125 here ends with 25.
Case Ii: 15²=225 and 15³= 3375 here ends with 75) For More learn
(iv) There is no perfect cube which ends with 8.
Answer: false
(Such as 12³=1728 ends with 8)
(v) The cube of a two digit number may be a three digit number.
Answer: false
(Because the smallest two digit number is 10 and it's cube, 10³= 1000, which is a four digit number.)
(vi) The cube of a two digit number may have seven or more digits.
Answer: false
(Because the largest two digit number is 99 and it's cube 99³=970299, which is a 6 digit number)
(vii) The cube of a single digit number may be a single digit number.
Answer: true.
(Such as 2³=8 is a one digit number
4³=16 is a two digit number)
Question 3:
You are told that 1,331 is a perfect cube. Can you guess with factorization what is its cube root? Similarly guess the cube roots of 4913, 12167, 32768.
Answer 3:
(i) First we divide the digits into group of three digits from rightmost side. Now we get two groups. First group has digit 331 and second group has digit 1.
Since fast group has 1 in its unit place so the cube root number has digit 1 at its unit place because 1³=1
In second group the number is 1. We know that 1³=1
Therefore the digit of 10 place of cube root number is 1
Hence cube root of 1331 is 11
(learn how to cube number)
(ii) cube root of number 4913?
First we divide the digits into groups of three digit. Now we get two groups, first group has number 913 and second group has number only 4.
Since there is 3 at unit place of 913 therefore the cube root number has 7 in its unit place because 7³=343.
The second group has number 4. Now 1³=1, 2³=8. 1 < 4 < 8. Since 1 is nearer to 4 then 8. Therefore what is the digit at tens place of cube root number.
Therefore cube root of 4913 is 17.
(iii) 12167
We divide the digits into group of three digits
We get two groups. First group has number 167 and second group has number 12.
Since there is seven at one place in first group so so there is 3 at one's place of the cube root number because 3³=27.
In second group there is the number 12. 2³=8 and 3³=27.
8 < 12 < 27
8 is nearer to 12 then 27. Therefore at 10 place there is 2 of cube root number.
Hence the cube root of number 12167 is 23
(iv) 32768
first we divide the digits into groups of three digits. We get two groups. First group has number 768 and second group has number 32.
since there is 8 at one place of first group number so there is two at unit place of cube root number because 2³=8.
Second group has number 32.
3³=27,. 4³=64
27 < 32 < 64
27 is nearer to 32 than 64.
Therefore there is 3 at ten place of cube root number.
Hence the cube root number of 32768 is 32.