Polygons CBSE Class 8
What is Polygon?
7J72I6DH
More Important Searches For You
CBSE Factorisation Mathematics Class VIII(8TH)
Cell: Structure and Function Class VIII CBSE
CBSE Factorisation Mathematics Class VIII(8TH)
Friction CBSE Class VIII
Probability CBSE Maths
Area of Trapezium, CBSE
Visit My Site Regularly For More New Update on CBSE NCERT CLASS
a plane
figure with at least three straight sides and angles, and typically five or
more.
Example
of Polygons:
Triangle,
quadrilateral, pentagon, hexagon, heptagon, octagon, nonagon, decagon according
as it contains 3,4,5,6,7,8,9,10 sides respectively.
Different
types of polygons:
Concave Polygon: A polygon which has at least one
angle is greater than 180° is called concave polygon.
Convex Polygon: A polygon in which all the angles
are less than 180° is called convex polygon.
Regular Polygon: A polygon in which all sides and
all angles are equal is called regular polygon. Example: equilateral triangle,
square.
Irregular Polygon: A polygon in which all sides and
all angles are not equal is called irregular polygon. Example: rectangle,
rhombus.
1. Find the measure of each
exterior angle of a regular (i)
triangle (ii) 4 sides polygon (iii) Pentagon (iv) 10 sides polygon (v) 15 sides polygon.
Answer:
(i) Each
exterior angle of a regular triangle ( equilateral triangle) = (360/3)= 120°
(ii) Each
exterior angle of a regular polygon of sides 4 = (360/4) = 90°
(iii) Each
exterior angle of a regular pentagon = (360/5) = 72°
(iv) Each
exterior angle of a regular polygon of sides 10 = (360/10) = 36°
(v) Each
exterior angle of a regular polygon of sides 15 = (360/15) = 24°
You may Like
2. Is it possible to have a
regular polygon each of whose exterior angles is (i) 60° (ii) 55°?
Answer:
(i) Let the
number of sides of given polygon be n
Therefore,
each of its exterior angle = (360/n)°
Now, (360/n)
= 60
→ n= 360/60
→ n= 6 (which is a whole number)
So, it is
possible to have a regular polygon each of whose exterior angles is 60°
(ii) Let the number of sides of given polygon be n
Therefore,
each of its exterior angle = (360/n)°
Now, (360/n)
= 55
→ n = (360/55)
→ n = 72/11 (which is not a whole number)
So, it is
not possible to have a regular polygon each of whose exterior angles is 55°
3. Find the measure of each interior angle
of a regular polygon having (i) 10
sides (ii) 15 sides (iii) 8 sides.
Answer:
(i) Sum of all exterior angles = 360°
Each exterior angle = (360/10) = 36°
Therefore, each interior angle =
(180-36) = 144°
(ii) Sum of all exterior angles = 360°
Each exterior angle = (360/15) = 24°
Therefore, each interior angle =
(180-24) = 156°
(iii) Sum of all exterior angles =
360°
Each exterior angle = (360/8) = 45°
Therefore, each interior angle = (180-45)
= 135°
(4) Is it possible to have a regular
polygon each of whose interior angles is 100°?
Answer:
Each interior angle = 100°
Each exterior angle = (180-100) = 80°
Sum of all exterior angles = 360°
Therefore, Number of sides = (360/80)
= (9/2)
(which is not a whole number)
It is not possible.
5. What is the sum of all interior angles
of a regular (i) pentagon (ii) hexagon
(iii) heptagon?
Answer:
(i) Sum of all interior angles of a
regular pentagon = (2 x 5 - 4)
right angles
= 6 right angles
(ii) Sum of all interior angles of a
regular hexagon
= (2
x 6 - 4) right angles
= 8 right angles
(iii) Sum of all interior angles of a
regular heptagon
= (2
x 7 - 4) right angles
= 10 right angles
6. What is the number of diagonals in
a (i) pentagon (ii) hexagon
(iii) polygon of 12 sides?
Answer:
(i) Number of diagonals of a polygon
of n sides = [n(n-3)/2]
Therefore, number of diagonals of a
pentagon = [5(5-3)/2] = 5
(ii) number of diagonals of a pentagon
= [6(6-3)/2] = 9
(iii) number of diagonals of a
pentagon
= [12(12-3)/2] = 54
7. Find the number of sides of a regular
polygon whose each exterior angles measures
(i) 40° (ii) 60° (iii) 90°
Answer:
(i) Sum of all exterior angles of a
regular polygon = 360°
Each exterior angle = 40°
Therefore, number of exterior angles =
(360/40) = 9
Number of sides of that regular
polygon = 9
(ii) Sum of all exterior angles of a
regular polygon = 360°
Each exterior angle = 60°
Therefore, number of exterior angles =
(360/60) = 6
Number of sides of that regular
polygon = 6
(iii) Sum of all exterior angles of a
regular polygon = 360°
Each exterior angle = 90°
Therefore, number of exterior angles =
(360/90) = 4
Number of sides of that regular
polygon = 4
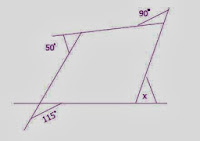
8. In the given figure find the measure
‘x’.
Answer: Sum of all exterior angles of
a polygon = 360°
Therefore, 50+115+90+x = 360
→ x = 105°
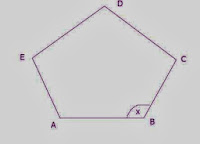
9. Find the angle measure ‘x’ in the given
figure.
Answer: Sum of all interior angles of
a polygon
= (2
x 5 - 4)
right angles
= 6 right angles
= 6
x 90°
Since this is a regular pentagon
Therefore, x = (6 x
90°)/ /5
→ x = 108°
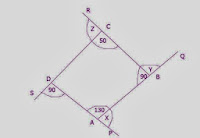
10. Find the value of (x+y+z)
Answer:
Exterior angle + interior adjacent
angle = 180°
X = (180 – 130) = 50°
Y = (180 – 90 ) = 90°
Z = (180 – 50) = 130°
(x+y+z) = 50+90+130 = 270°
Some Important Formulas of Polygon:
(i) Sum of all exterior angles = 360°
(ii) Each exterior angle = (360/n)° [n = number of sides]
(iii) Each interior angle = 180° - (each exterior angle)
(iv) Sum of all interior angles = (2n - 4) right angles
(v) Number of diagonals in a polygon of n sides = n(n-3)/2
More Important Searches For You
CBSE Factorisation Mathematics Class VIII(8TH)
Cell: Structure and Function Class VIII CBSE
CBSE Factorisation Mathematics Class VIII(8TH)
Friction CBSE Class VIII
Probability CBSE Maths
Area of Trapezium, CBSE
Visit My Site Regularly For More New Update on CBSE NCERT CLASS