CBSE Class VIII Maths Area of Polygon
Area of Polygon CBSE
Class VIII Maths
The plots
and fields are in the form of regular or irregular polygons. We find their
areas by dividing them into triangles, rectangles, parallelograms and
trapeziums.
1. In the give figure, PQRS is a
quadrilateral in which PR=32m, QX perpendicular PR, SY perpendicular PR such that QX=10m and
SY=8m. Find the area of the quad PQRS.
Area of quad PQRS = Area of ∆PQR +
Area of ∆SPR
= (½ x
PR x QX) + (½
x PR x
SY)
= (½ x
32 x 10) + (½
x 32 x 8)
= 160 + 128
= 288 cm²
You may Like
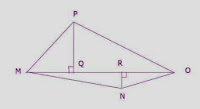
2. In the give figure,
MNOP is a quadrilateral-shaped field in which diagonal MO= 18 cm, PQ perpendicular
MO, NR perpendicular MO such that PQ=7cm and NR=3cm. Find the area of the quad
MNOP.
Answer:
Area of quad
MNOP = Area of ∆MNO + Area of ∆MPO
= (½ x MO
x RN) + (½ x MO
x PQ)
= (½
x 18 x 3m) + (½
x 18 x 7)
= 27 + 63
= 90 cm²
3. Find the area of pentagon PQRST
in which QM perpendicular PR, SN perpendicular PR, TO perpendicular PR such that
PR=24m, PN=18m, PO=10m, QM=5m, SN=9m, TO=7m.
Answer:
Area of
pentagon PQRST= Area of ∆PQR + Area of ∆SNR + Area of quad
TONS + Area of ∆TOP
= (½ x PR
x QM) + (½ x NR
x SN) + {½ X (SN+TO)
x ON} + (½ x PO
x TO)
= (½ x 24
x 5) + (½ x 6
x 9) + {½ X (9+7)
x 8} + (½ x 10
x 7)
= 60 + 27 +
64 + 35
=186 m²
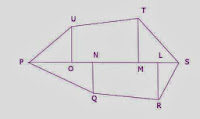
4. Find the area of hexagon PQRSTU
in which QN perpendicular PS, RL perpendicular PS, TM perpendicular PS, UO
perpendicular PS such that PO= 4m, ON=2m, NM= 6m, ML=2m, LS= 6m, UO= 6m, TM=
8m, QN= 2m, RL=4m.
Answer:
Area of the
hexagon PQRSTU = Area of ∆PQN + Area of quad QRLN + Area of ∆RSL + Area of ∆TLS + Area of quad
OMTU + Area of ∆POU
= (½ x PN
x QN) + {½ X (RL+QN)
x NL} + (½ x LS
x RL) + (½ x MS
x TM) + {½ X (TM+UO)
x OM} + (½ x PO
x UO)
= (½ x 6
x 2) + {½ X (4+2)
x 8} + (½ x 6
x 4) + (½ x 8
x 8) + {½ X (8+6)
x 8} + (½ x 4
x 6)
= 6 + 24 +
12 + 32 + 56 + 12
= 142 m²
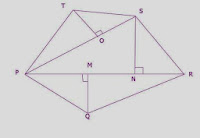
5. Find the area of pentagon PQRST
in which QM perpendicular PR, SN perpendicular PR, TO perpendicular PS such
that PR=24m, PS=28m, QM=10m, SN=14m, TO=6m.
Answer:
Area of
pentagon PQRST = Area of ∆PQR + Area of ∆SPR + Area of ∆TPS
= (½ x PR
x QM) + (½ x PR
x SN) + (½ x PS
x TO)
= (½ x 24 x 10) +
(½ x 24
x 14) + (½ x 28
x 6)
= 120 + 168
+ 84
= 372 m²
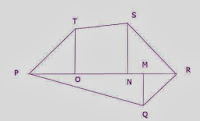
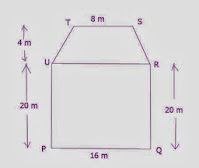
6. Find the area of the adjacent
figure PQRST.
Answer:
Area of
PQRSTU = Area of rectangle PQRU + Area of trapezium RSTU
= (RQ x PQ)
+ {½ x (UR+TS)
x height)
= (20 x 16)
+ {½ x (16+8)
x 4)
= 320 + 48
= 368 m²
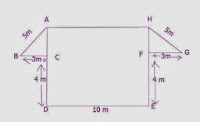
7. Find the area of the adjacent
figure ABCDEFGH.
Answer:
∆ABC is a right angled triangle and its base BC=3 m and
hypotenuse AB=5m.
Therefore,
AC²= AB² - BC²
= 5² - 3²
AC = 4m
Similarly,
HF=4m
Area of
ABCDEFGH = Area of rectangle ADEH + Area of ∆ABC + Area of ∆HFG
= (AD
x DE) + (½ x BC
x AC) + (½
x FG x
HF)
= (8
x 10) + (½ x 3
x 4) + (½
x 3 x
4)
= 80 + 6 + 6
= 92 m²
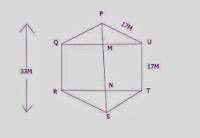
8. Find the area of the adjacent
regular hexagon PQRST in which each side measures 17m and its height is 33m.
Answer:
From the
figure, MN=UT=QR=17m
Therefore,
PM=NS=½ (33-17)
= ½ x 16
= 8m
Therefore,
MU=QM= √17²‾-‾8²‾
= 15m
QU=RT= 2 x 15
= 30m
Area of hexagon PQRSTU = Area of ∆PQU
+ Area of rectangle QRTU + Area of ∆RST
= (½
x QU x PM)+
(RT x
RQ)+(½ x RT
x NS)
= (½ x 30
x 8)+ (30 x 17)+(½ x 30
x 8)
= 120 + 510
+ 120
= 750 m²
More Important Searches For You
CBSE Factorisation Mathematics Class VIII(8TH)
Cell: Structure and Function Class VIII CBSE
CBSE Factorisation Mathematics Class VIII(8TH)
Friction CBSE Class VIII
Probability CBSE Maths
Area of Trapezium, CBSE
Visit My Site Regularly For More New Update on CBSE NCERT CLASS
More Important Searches For You
CBSE Factorisation Mathematics Class VIII(8TH)
Cell: Structure and Function Class VIII CBSE
CBSE Factorisation Mathematics Class VIII(8TH)
Friction CBSE Class VIII
Probability CBSE Maths
Area of Trapezium, CBSE
Visit My Site Regularly For More New Update on CBSE NCERT CLASS